战争雷霆坦克弹种选择推荐 坦克护甲防御弱点及摆角度攻略

2.余弦定理

　　护甲的余弦定理，总是在提，具体如何那，用网上找的一段资料来给大家看看。

　　穿透甲板是一复杂过程。以动能形式穿甲时，甲板经受了高速的应变、应力和压力由此会造成甲板结构和性能发生变化。对此，本章不拟细述，只要把穿甲机理理解为与冶金加工现象类似就足够了。

　　如前述，为实现穿甲，弹丸必须在小面积上集中高能量(即mv^2／d^2值很高)。如果把对弹丸的这种能量要求与弹丸沿法线方向(射向与直立平甲板的板面呈90°)可以穿透的甲板厚度(T)联系起来，则可用下式

　　T／d=mv^2／d^3

　　计算穿甲弹性能。该式被称为“基本穿甲方程”，表示所用弹丸每单位口径能穿透的甲板厚度。

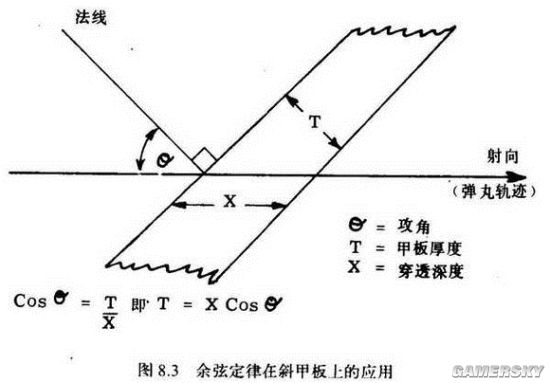
　　弹丸射向不沿法线方向时，计算其穿甲性能较为复杂。如图8.3所示，一眼就能看出可按余弦定理进行计算。

　　余弦定理在斜甲板上的应用

　　但实际上若弹丸以斜角射向甲板，它并不遵循余弦定理。这时，弹丸被迫沿“S”形轨迹而不是直线地穿过甲板。有很多复杂公式可计算弹丸斜角穿甲性能，其中最著名的是米尔尼－德－玛丽公式。用这些公式计算穿甲性能低于按余弦定理所计算的结果。但实际上现代穿甲弹的穿甲性能却比按余弦定理计算的结果稍高。例如，使用转动被帽就会使穿甲弹的穿甲性能优于按余弦定理计算值。如图8.4所示，穿甲弹斜向射击甲板时会变向，并从甲板跳飞；但若配用转动被帽，则只有被帽在撞击时才做跳飞运动，而被帽的运动却迫使穿甲弹弹体在开始穿透甲板前便转为与甲板垂直。

　　以上摘自互联网。

更多相关资讯请关注：战争雷霆专区